Contents
sys = mr.opts('MaxGrad',32,'GradUnit','mT/m',...
'MaxSlew',130,'SlewUnit','T/m/s',...
'rfRingdownTime', 30e-6, 'rfDeadtime', 100e-6,...
'adcDeadTime', 10e-6, 'B0', 2.89 ...
);
seq=mr.Sequence(sys);
fov=256e-3; Nx=64; Ny=Nx;
thickness=4e-3;
sliceGap=1e-3;
Nslices=8;
pe_enable=1;
ro_os=1;
readoutTime=4.2e-4;
partFourierFactor=1;
sat_ppm=-3.45;
sat_freq=sat_ppm*1e-6*sys.B0*sys.gamma;
rf_fs = mr.makeGaussPulse(110*pi/180,'system',sys,'Duration',8e-3,'dwell',10e-6,...
'bandwidth',abs(sat_freq),'freqOffset',sat_freq,'use','saturation');
rf_fs.phaseOffset=-2*pi*rf_fs.freqOffset*mr.calcRfCenter(rf_fs);
gz_fs = mr.makeTrapezoid('z',sys,'delay',mr.calcDuration(rf_fs),'Area',0.1/1e-4);
[rf, gz, gzReph] = mr.makeSincPulse(pi/2,'system',sys,'Duration',2e-3,...
'SliceThickness',thickness,'apodization',0.42,'timeBwProduct',4,'use','excitation');
trig=mr.makeDigitalOutputPulse('osc0','duration', 100e-6);
deltak=1/fov;
kWidth = Nx*deltak;
blip_dur = ceil(2*sqrt(deltak/sys.maxSlew)/10e-6/2)*10e-6*2;
gy = mr.makeTrapezoid('y',sys,'Area',-deltak,'Duration',blip_dur);
extra_area=blip_dur/2*blip_dur/2*sys.maxSlew;
gx = mr.makeTrapezoid('x',sys,'Area',kWidth+extra_area,'duration',readoutTime+blip_dur);
actual_area=gx.area-gx.amplitude/gx.riseTime*blip_dur/2*blip_dur/2/2-gx.amplitude/gx.fallTime*blip_dur/2*blip_dur/2/2;
gx.amplitude=gx.amplitude/actual_area*kWidth;
gx.area = gx.amplitude*(gx.flatTime + gx.riseTime/2 + gx.fallTime/2);
gx.flatArea = gx.amplitude*gx.flatTime;
adcDwellNyquist=deltak/gx.amplitude/ro_os;
adcDwell=floor(adcDwellNyquist*1e7)*1e-7;
adcSamples=floor(readoutTime/adcDwell/4)*4;
adc = mr.makeAdc(adcSamples,'Dwell',adcDwell,'Delay',blip_dur/2);
time_to_center=adc.dwell*((adcSamples-1)/2+0.5);
adc.delay=round((gx.riseTime+gx.flatTime/2-time_to_center)*1e6)*1e-6;
gy_parts = mr.splitGradientAt(gy, blip_dur/2, sys);
[gy_blipup, gy_blipdown,~]=mr.align('right',gy_parts(1),'left',gy_parts(2),gx);
gy_blipdownup=mr.addGradients({gy_blipdown, gy_blipup}, sys);
gy_blipup.waveform=gy_blipup.waveform*pe_enable;
gy_blipdown.waveform=gy_blipdown.waveform*pe_enable;
gy_blipdownup.waveform=gy_blipdownup.waveform*pe_enable;
Ny_pre=round(partFourierFactor*Ny/2-1);
Ny_post=round(Ny/2+1);
Ny_meas=Ny_pre+Ny_post;
gxPre = mr.makeTrapezoid('x',sys,'Area',-gx.area/2);
gyPre = mr.makeTrapezoid('y',sys,'Area',Ny_pre*deltak);
[gxPre,gyPre,gzReph]=mr.align('right',gxPre,'left',gyPre,gzReph);
gyPre = mr.makeTrapezoid('y',sys,'Area',gyPre.area,'Duration',mr.calcDuration(gxPre,gyPre,gzReph));
gyPre.amplitude=gyPre.amplitude*pe_enable;
slicePositions=(thickness+sliceGap)*((0:(Nslices-1)) - (Nslices-1)/2);
slicePositions=slicePositions([1:2:Nslices 2:2:Nslices]);
for s=1:Nslices
seq.addBlock(rf_fs,gz_fs);
rf.freqOffset=gz.amplitude*slicePositions(s);
rf.phaseOffset=-2*pi*rf.freqOffset*mr.calcRfCenter(rf);
seq.addBlock(rf,gz,trig);
seq.addBlock(gxPre,gyPre,gzReph);
for i=1:Ny_meas
if i==1
seq.addBlock(gx,gy_blipup,adc);
elseif i==Ny_meas
seq.addBlock(gx,gy_blipdown,adc);
else
seq.addBlock(gx,gy_blipdownup,adc);
end
gx.amplitude = -gx.amplitude;
end
end
check whether the timing of the sequence is correct
[ok, error_report]=seq.checkTiming;
if (ok)
fprintf('Timing check passed successfully\n');
else
fprintf('Timing check failed! Error listing follows:\n');
fprintf([error_report{:}]);
fprintf('\n');
end
Timing check passed successfully
do some visualizations
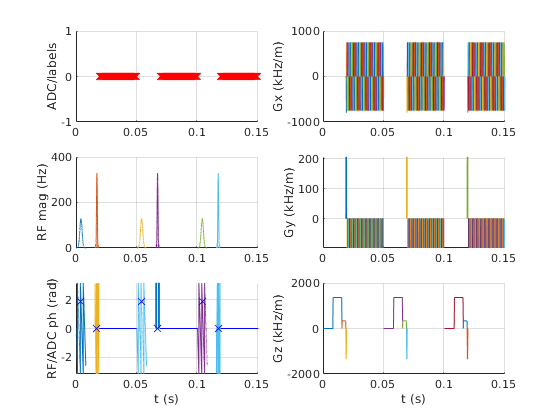
seq.plot();
seq.plot('timeDisp','us','showBlocks',1,'timeRange',[0 25e-3]);
rf.freqOffset=0;
rf.phaseOffset=0;
[rf_bw,rf_f0,rf_spectrum,rf_w]=mr.calcRfBandwidth(rf);
figure;plot(rf_w,abs(rf_spectrum));
title('Excitation pulse profile (low-angle approximation)');
xlabel('Frequency, Hz');
xlim(3*[-rf_bw rf_bw]);
trajectory calculation
[ktraj_adc, t_adc, ktraj, t_ktraj, t_excitation, t_refocusing, slicepos, t_slicepos] = seq.calculateKspacePP();
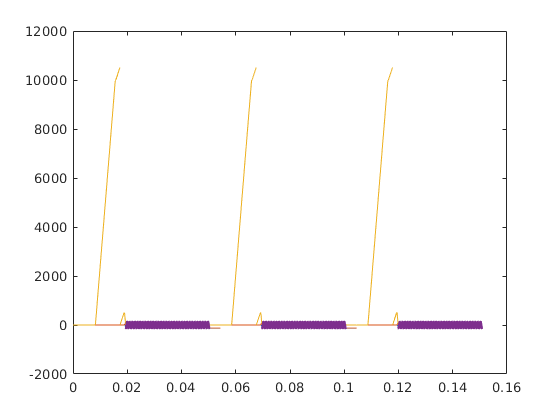
figure; plot(t_ktraj, ktraj');
hold on; plot(t_adc,ktraj_adc(1,:),'.');
title('k-space vector components as functions of time');
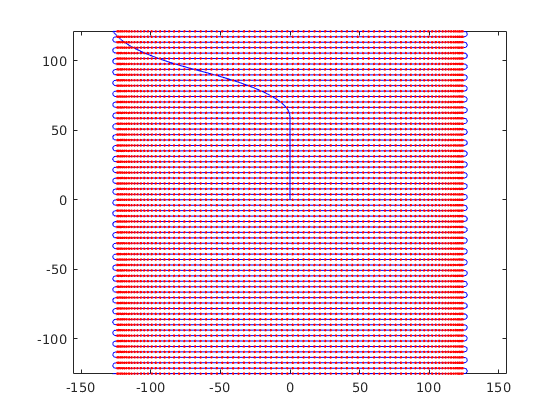
figure; plot(ktraj(1,:),ktraj(2,:),'b');
hold on;plot(ktraj_adc(1,:),ktraj_adc(2,:),'r.');
axis('equal');
title('k-space trajectory (k_x/k_y)');
figure; plot(t_slicepos, slicepos, '*');
title('slice position (vector components) as a function or time');



prepare the sequence output for the scanner
seq.setDefinition('Name', 'epi');
seq.setDefinition('FOV', [fov fov max(slicePositions)-min(slicePositions)+thickness]);
seq.setDefinition('ReceiverGainHigh',1);
seq.write('epi_rs.seq');
return;
another manual pretty plot option for gradients
lw=1.2;
wave_data=seq.waveforms_and_times(true);
gwm=max(abs([wave_data{1:3}]'));
rfm=max(abs([wave_data{4}]'));
ofs=2.05*gwm(2);
figure;
axis_clr=[0.5,0.5,0.5];
plot([-0.01*gwm(1),1.01*gwm(1)],[0 0]*ofs,'Color',axis_clr,'LineWidth',lw/5); hold on;
plot([-0.01*gwm(1),1.01*gwm(1)],[1 1]*ofs,'Color',axis_clr,'LineWidth',lw/5);
plot([-0.01*gwm(1),1.01*gwm(1)],[2 2]*ofs,'Color',axis_clr,'LineWidth',lw/5);
plot([-0.01*gwm(1),1.01*gwm(1)],[3 3]*ofs,'Color',axis_clr,'LineWidth',lw/5);
wave_data{4}(2,wave_data{4}(2,:)==0)=NaN;
plot(wave_data{4}(1,:), real(wave_data{4}(2,:))/rfm(2)*gwm(2)*0.75+3*ofs,'k','LineWidth',lw);
plot(wave_data{3}(1,:), wave_data{3}(2,:)+2*ofs,'Color',[0,0.5,0.3],'LineWidth',lw);
plot(wave_data{2}(1,:), wave_data{2}(2,:)+1*ofs,'r','LineWidth',lw);
plot(wave_data{1}(1,:), wave_data{1}(2,:),'b','LineWidth',lw);
t_adc_gr=t_adc+0.5*seq.gradRasterTime;
gwr_adc=interp1(wave_data{1}(1,:), wave_data{1}(2,:),t_adc_gr);
plot(t_adc_gr,gwr_adc,'b.','MarkerSize',5*lw);
xlim([-0.03*gwm(1),1.03*gwm(1)]);
set(gca,'xtick',[]);
set(gca,'xticklabel',[]);
set(gca,'ytick',[]);
set(gca,'yticklabel',[]);
very optional slow step, but useful for testing during development e.g. for the real TE, TR or for staying within slew rate limits
rep = seq.testReport;
fprintf([rep{:}]);
return
create a smoothly rotating 3D k-space plot
[kfa,ta,kf]=seq.calculateKspacePP();
figure;plot3(kf(1,:),-kf(3,:),kf(2,:));
hold on;plot3(kfa(1,:),-kfa(3,:),kfa(2,:),'r.');
set(gca,'visible','off');
set(gca, 'CameraViewAngle',get(gca, 'CameraViewAngle'));
kabsmax=max(abs(kf)')';
kxyabsmax=max(kabsmax([1 3]));
kxyzabsmax=max(kabsmax);
axis(0.01*[-kxyzabsmax kxyzabsmax -kxyzabsmax kxyzabsmax -kxyzabsmax kxyzabsmax])
[caz,cel] = view;
folder='kspace3d';
mkdir(folder);
for caz_add=0:5:359
view(caz+caz_add,cel);
drawnow;
end





